
数据分析常用算法解析—聚类分析(上)
作者:重山智业来源:www.chongshanzy.com时间:2023-07-03 09:46:26阅读:896
某市有大约180个卷烟品规,这些卷烟在品牌、销售量和销售额方面存在巨大差异。因此,该市的公司希望按照一定的标准将这180个产品划分为四个等级,以便公司能够采取差异化品牌培育措施。那么,该公司应该如何操作呢?很多人可能会想到使用波士顿矩阵(Boston Matrix),以销售量和销售额作为横纵坐标轴,并计算中心轴,将每个产品落入矩阵中,以得到大致的产品分类情况。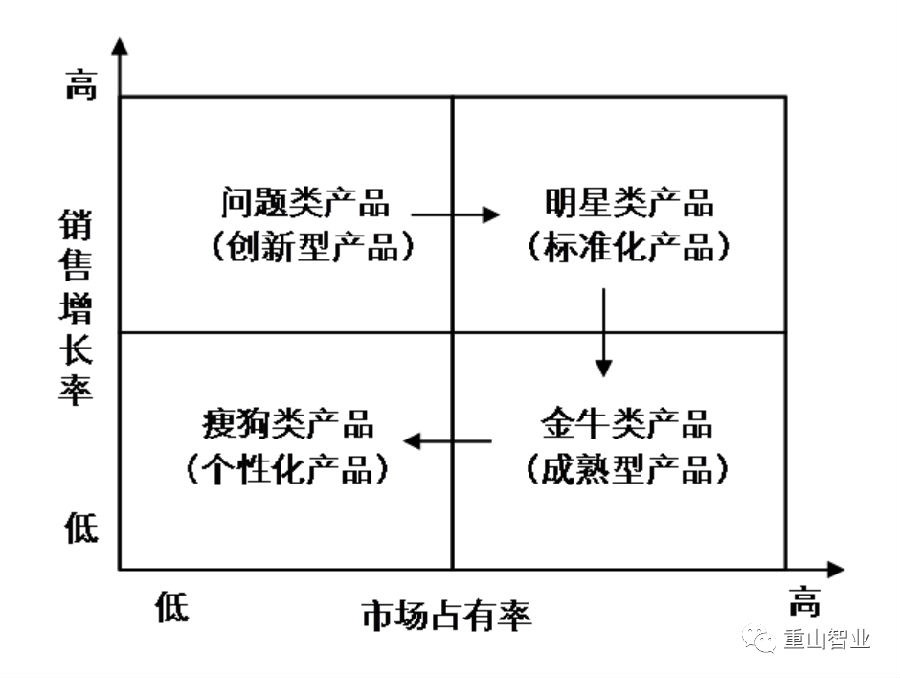
看上去好像没有问题,对吗?但实际情况中,很多人使用这种方法却会得出错误的结果。为什么呢?事实上,这种思路是正确的,但很多人都忽略了一个最关键的问题:应该使用什么标准来衡量和判断中心轴的划分。许多人会选择直接使用数据的平均值作为中心轴,然而,在实际情况中,这种分类方法可能会导致数据的错误划分,因为不同类别的数据可能呈现出族群(cluster)的现象,这时候一些数据可能会"鱼目混珠"地混入其他类别中。举个极端的例子,假设有三个产品A、B、C的销售量分别为100、50、1,很显然,A、B产品属于同一类别,而C产品属于另一类别。然而,如果按照平均值151/3=50.03来划分,就会将A划分到一类,而B和C划分到另一类。是不是很奇怪呢?这时候,我们就需要使用到今天要介绍的分类分析方法——聚类(clustering)了。聚类原本是统计学上的概念,如今已属于机器学习中非监督学习的范畴,广泛应用于数据挖掘和数据分析领域。简单来说,聚类可以用一个词概括——物以类聚。如果将人和其他动物放在一起进行比较,你可以轻松找到一些判断特征,比如肢体、嘴巴、耳朵、皮毛等等。根据这些判断指标之间的差距大小,你可以将它们划分为不同的类别,比如人类、狗类、鱼类等等,这就是聚类的基本思想。从定义上来讲,聚类是针对大量数据或样本,根据数据本身的特性研究分类方法,并按照这个分类方法对数据进行合理的分类。最终,相似的数据被归为同一组,实现了"同类相同、异类相异"的原则。分类是按照预定的程序模式和标准进行判断和划分。就像我们前面提到的例子,我们直接规定将数据的平均值作为中心轴,然后只需判断每个数据是否达到平均值。换句话说,在进行分类之前,我们已经有了一套固定的数据划分标准,只需按照标准严格将数据分组即可。然而,聚类则不同。我们并不知道具体的划分标准,需要依靠算法来判断数据之间的相似性,将相似的数据放在一起。也就是说,聚类的关键工作是探索和挖掘数据中的潜在差异和联系。在聚类的结果出来之前,我们完全不知道每个类别具有什么特点。必须根据聚类的结果,通过人的经验来分析,看看聚成的每个类别大致有哪些特点。了解了聚类的含义,接下来我们要具体了解如何对数据进行聚类。在数据分析中,常用的聚类方法之一是K-Means聚类法。这种方法既简单又有效,并且在许多分析软件中都可以进行算法计算。下面用一个例子来介绍K-Means聚类法的原理和过程:K-Means聚类法中的K表示要得到的分组数目,即我们希望通过聚类得到多少个组类。举个例子,假设我们有以下六个数据,想将它们分成两类,那么K=2。
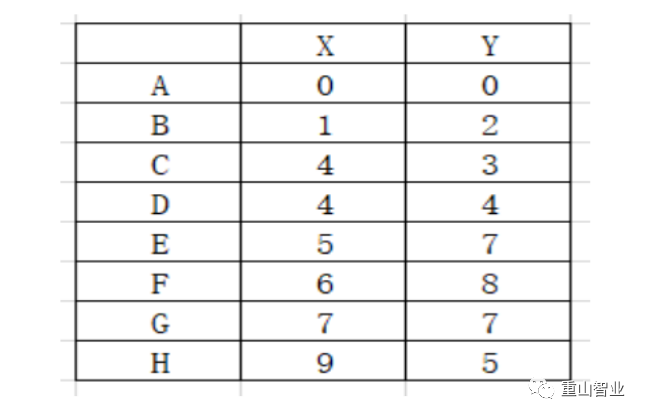
这些数据中心的选择是完全随机的,也就是说选择的方式并不重要。因为这里K=2,所以我们随机选择两个数据点作为数据中心,例如选择A和B。为了便于理解,绘制一个散点图,并将A和B作为数据中心。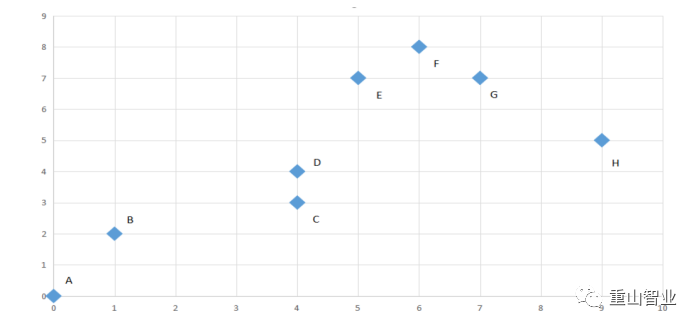
既然选择了数据中心,那么周围一定会有很多相似的数据。如何判断这些数据与数据中心的相似性呢?可以用欧拉距离来计算。简单来说,欧氏距离是多维空间中两个点之间的绝对距离,用于衡量两点之间的远近。其公式如下: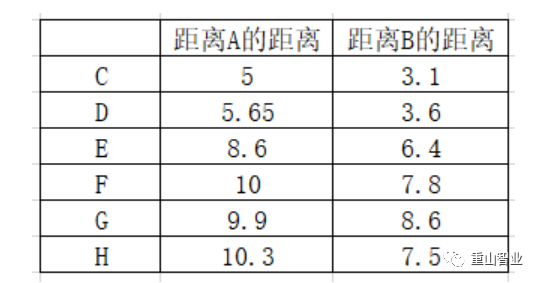
所以,根据计算结果,C 到 H 的距离都比距离 A 近,因此第一次分组结果如下:获得第一次分组的结果后,我们重复前两个步骤,重新选择每个组别的数据中心。而第二组有 7 个数据点,我们计算这 7 个数据点的坐标平均值,得到新的数据中心 P,其坐标为(5.14, 5.14)。同样使用欧氏距离计算其他数据与数据中心 A 和 P 的距离,结果如下: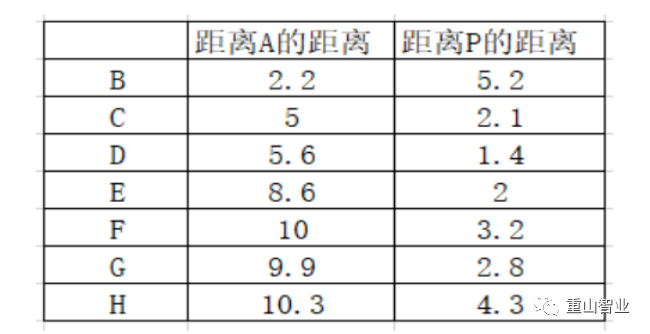
根据计算结果,有些数据点更接近 A,有些更接近 P。因此,第二次分组结果如下:第二组:C、D、E、F、G、H
未完待续……















 位访客!
位访客!
